La sezione aurea
La progressione di Fibonacci, non è solo un gioco né riguarda solo l’economia: descrive un modello di crescita naturale, un ordine nascosto che lega matematica e natura e che è presente in ogni cosa che riteniamo “bella” e che diventa simbolo di armonia universale. È un esempio perfetto di come un calcolo pratico possa trasformarsi in mito culturale. È strettamente legata alla “sezione aurea” che è un numero che descrive una proporzione percepita dall’uomo come armoniosa. Il nome “aurea” fu introdotto in epoca moderna, in particolare nel XIX secolo, ma la proporzione era già nota agli antichi Greci e, nel Rinascimento, fu celebrata da Luca Pacioli come “Divina Proportione”.
La sezione aurea si ottiene dividendo un segmento in due parti in modo che:
segmento totale sta alla parte maggiore come la parte maggiore sta a quella minore
in formule se indichiamo con “a” il segmento maggiore e con “b” il minore, la definizione si trascrive come
(a+b) : a = a : b
cioè:
1 + b/a = a/b
Il rapporto “a/b” risultante fra i due segmenti è un numero irrazionale, indicato con la lettera greca φ (phi), pari a circa 1,618033…. che è detto anche “numero aureo”, “proporzione aurea”, “rapporto aureo”.
Già Euclide (III sec. a.C.) descriveva la “divisione in estrema e media ragione” nei suoi “Elementi”. La scuola pitagorica la considerava simbolo di armonia. Luca Pacioli, nel 1509, la celebrò nel trattato “De Divina Proportione”, illustrato da Leonardo da Vinci, collegandola alla bellezza e all’arte. L’espressione “sezione aurea” si diffuse solo nell’Ottocento, quando matematici e storici dell’arte iniziarono a chiamarla così per sottolinearne il valore estetico e “prezioso”. L’associazione con la lettera Φ (phi) deriva dal nome dello scultore greco Fidia, che si riteneva avesse usato questa proporzione nei suoi capolavori.
La sezione aurea compare in molti capolavori dell’arte e dell’architettura:
Piramide di Cheope (2550 a.C.): il rapporto tra l’altezza dell’apotema e metà della base richiama φ.
Partenone di Atene (V sec. a.C.): proporzioni della facciata e delle colonne vicine al rapporto aureo.
Cattedrali gotiche: i rosoni e le facciate rispettano proporzioni auree per trasmettere armonia.
Leonardo da Vinci: nell’ “Uomo Vitruviano” e nelle illustrazioni del trattato “De Divina Proportione” di Luca Pacioli, la sezione aurea è centrale.
Sandro Botticelli: nella Nascita di Venere la disposizione delle figure segue proporzioni auree.
Piero della Francesca: studi matematici e pittorici basati sulla proporzione aurea.
Salvador Dalí: in La Ultima Cena (1955) la struttura del dipinto è costruita su un dodecaedro aureo.
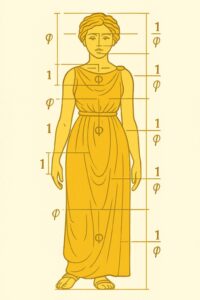
Un detto popolare recita; “altezza mezza bellezza”, ma in realtà ciò che rende piacevole e “bello” un corpo è avere le proporzioni che si avvicinino il più possibile alle proporzioni auree, come le cariatidi dell’Eretteo sull’acropoli di Atene o le bambole “Barbie”: la distanza dal capo all’ombelico e dall’ombelico ai piedi tende, larghezza della bocca rispetto alla larghezza del naso, distanza tra occhi e bocca rispetto all’intera lunghezza del volto, posizione degli occhi rispetto alla fronte e al mento, lunghezza dell’avambraccio rispetto alla mano, lunghezza delle falangi delle dita: ogni segmento è in rapporto aureo con il successivo, larghezza delle spalle rispetto alla lunghezza del torso, rapporto tra busto e gambe.
In fotografia
Anche nella fotografia la sezione aurea è impiegata come regola di composizione per guidare lo sguardo: le linee che si vedono nella inquadratura sono quelle della “regola dei terzi” che indicano i “punti forti”, ma si avvicinano molto alla sezione aurea.
La sezione aurea è una proporzione ideale, ma la regola dei terzi è una scorciatoia pratica: più semplice da applicare, più diffusa, più adatta alla fotografia quotidiana. La sezione aurea resta un riferimento per chi vuole creare immagini con un senso di armonia “naturale” e profonda, ma non è lo standard perché richiede più consapevolezza e tempo.
Per chiarirsi: i punti forti sono le intersezioni delle linee della griglia fotografica e indicano le zone dell’inquadratura dove l’occhio umano tende naturalmente a posarsi. Sono importanti perché il nostro sguardo è attratto da queste aree più che dal centro geometrico dell’immagine. Collocare il soggetto principale su un punto forte evita la rigidità del “tutto al centro” e crea movimento. Insomma i punti forti aiutano a bilanciare soggetto e sfondo, dando respiro all’immagine.
Un volto collocato su un punto forte cattura subito l’attenzione senza risultare statico. In paesaggi, l’orizzonte posto lungo una linea della griglia e un elemento (albero, barca, sole) su un punto forte rende la scena più naturale e bilanciata. Nella fotografia di strada, un soggetto in movimento collocato su un punto forte suggerisce direzione e dinamismo.
La sezione aurea è la “misura segreta della bellezza”, capace di dare equilibrio e armonia alle forme.
Fibonacci e la sezione aurea
Per comprendere la relazione fra la progressione di Fibonacci e la sezione aurea prendiamo la sequenza di Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34…) e facciamo il rapporto tra un termine e quello precedente. Si ottengono valori che si avvicinano sempre di più a φ (phi), cioè la sezione aurea:
3/2 = 1,5
5/3 = 1,6666…
8/5 = 1,6
13/8 = 1,625
21/13 = 1,615 …
… e così via, tendendo a 1,618…
In altre parole, la sequenza di Fibonacci converge alla sezione aurea.
La sequenza di Fibonacci è come una scala che sale verso la sezione aurea: ogni gradino (rapporto tra due numeri) si avvicina sempre di più a quella proporzione perfetta. La sezione aurea è il limite, la meta; la sequenza di Fibonacci è il percorso che ci porta lì.
Ecco la visualizzazione che mostra come i rapporti tra numeri consecutivi della sequenza di Fibonacci si avvicinano progressivamente alla sezione aurea:

La linea orizzontale del grafico rappresenta φ, mentre la curva dei rapporti mostra come la sequenza di Fibonacci “sale a gradini” verso quella proporzione perfetta.
I valori inizialmente oscillano (1,5 – 1,66 – 1,6…), ma, man mano che la sequenza cresce, i rapporti si stabilizzano sempre più vicino a φ ≈ 1,618. Questo dimostra in modo visivo che la sequenza di Fibonacci è un percorso che converge verso la sezione aurea, trasformando un semplice gioco numerico in una legge universale di armonia.
Riccardo Agresti



