Oggi 23 novembre, nella notazione anglosassone (che pone prima il mese e poi il giorno) è l’11/23 e qualcuno avrà notato l’inizio di una famosa sequenza numerica: quella di Fibonacci.

Ma perché questa sequenza è così importante da dedicargli addirittura una giornata specifica: oggi, il Fibonacci day?

In questo articoletto, diviso in due parti, illustreremo come sia iniziato tutto, quali conseguenze ha avuto sulla nostra vita quotidiana, sulla economia e che connessioni forti abbia con l’arte, con la Natura e la bellezza.

Leonardo Pisano

Leonardo Pisano, detto Fibonacci, nacque a Pisa nel XII secolo. Figlio di un mercante, viaggiò tra Mediterraneo e Nord Africa dove entrò in contatto con la matematica araba. La sua opera più celebre, il Liber Abaci (1202), introdusse in Europa il sistema numerico indo-arabico, rivoluzionando il calcolo e aprendo la strada alla modernità.

Prima del 1202, in Europa si usavano numeri romani e sistemi di calcolo macchinosi. Fibonacci mostrò come con nove cifre e lo zero si potesse scrivere qualsiasi numero in maniera più comoda di quelli precedentemente utilizzati e questo comportò la sostituzione progressiva degli scomodi numeri romani e dell’abaco, trasformando profondamente il commercio, la contabilità e la matematica occidentale. Lo “zefiro” (dal termine arabo ṣifr), cioè lo zero, fu una novità assoluta permettendo l’uso di algoritmi molto più rapidi (i calcoli “in colonna” che usiamo ancora oggi con carta e penna). Il “Liber abaci” non si limitava a spiegare le cifre, ma presentava metodi di calcolo, proporzioni, frazioni e problemi pratici: un vero e proprio manuale rivolto ai mercanti che permise di gestire conti, interessi e cambi con maggiore facilità. Non fu solo un libro di matematica: fu una rivoluzione culturale ed economica, che cambiò il modo di pensare i numeri e di organizzare la vita quotidiana. Un esempio perfetto di come un testo tecnico possa diventare mito culturale: un ponte tra civiltà differenti che ha trasformato la memoria collettiva.

Il problema dei conigli

Nel Liber Abaci, Fibonacci propose un quesito semplice ma geniale:

“Se una coppia di conigli viene posta in un campo chiuso, quanti conigli nasceranno in un anno, supponendo che ogni mese una coppia generi una nuova coppia, che diventa fertile dal secondo mese?”

Le regole del gioco sono quindi:

1. Si parte con una coppia di conigli appena nata.
2. Ogni coppia diventa fertile dopo un mese.
3. Ogni coppia fertile genera una nuova coppia ogni mese.
4. I conigli non muoiono mai.

Ecco cosa accade seguendo le regole indicate:

• Mese 1: abbiamo 1 coppia appena nata.
• Mese 2: abbiamo 1 coppia che ora è diventata fertile.
• Mese 3: nasce una nuova coppia quindi siamo a 2.
• Mese 4: la prima coppia, quella originaria, genera ancora, mentre la seconda diventa fertile, siamo a 3 coppie presenti.
• Mese 5: entrambe le coppie generano per cui siamo a 3 precedenti più 2 nuove appena nate, siamo a 5 coppie.
• Mese 6: ora le 3 precedenti generano ancora (3 coppie nuove) e le 2 del mese precedente diventano fertili e siamo a 8 coppie.
• … e così via per cui ogni mese abbiamo le coppie presenti nel mese precedente cui si aggiungono nuove coppie derivanti dalla generazione delle coppie presenti nel mese antecedente (perché quelle appena generate sono diventate fertili, ma la gestazione dura un mese).

Matematicamente la regola si esprime semplicemente:

F(n) = F(n-1) + F(n-2)

dove “F(n)” indica il numero di Fibonacci, cioè coppie di conigli presenti al mese numero “n” e chiaramente “n-1” e “n-2” indicano le coppie presenti rispettivamente nel mese precedente e in quello antecedente: ogni mese il numero di coppie è la somma delle coppie del mese precedente e di quelle di due mesi prima.

Utilizzo in economia

Oggi, quella stessa sequenza è entrata nelle sale di trading e nei grafici delle borse mondiali. Gli analisti tecnici usano linee di ritracciamento di Fibonacci per individuare zone di supporto e resistenza, punti in cui il prezzo di un titolo può fermarsi o invertire la sua corsa. Percentuali come 23,6%, 38,2%, 61,8% derivano direttamente dai rapporti della sequenza e vengono usate per prevedere movimenti di mercato.

La forza di Fibonacci in economia, però, non sta in una legge naturale immutabile, ma in un fenomeno psicologico: milioni di trader guardano a quei livelli e proprio questa attenzione collettiva li rende significativi. È una sorta di “profezia che si autoavvera”, dove la matematica diventa linguaggio condiviso e influenza reale.

La spirale di Fibonacci

La spirale di Fibonacci è una costruzione geometrica che rende visibile il legame tra la progressione (cioè questo tipo particolare di sequenza in cui i termini seguono una regola precisa) e la Natura.

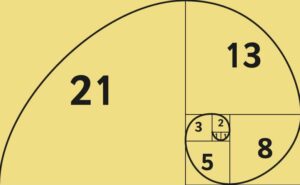
1. Si parte dalla sequenza di Fibonacci: 1, 1, 2, 3, 5, 8, 13…
2. Si costruiscono quadrati con lati lunghi quanto i numeri della sequenza.
   • Un quadrato di lato 1, accanto un altro di lato 1.
   • Sopra, un quadrato di lato 2.
   • Poi uno di lato 3, uno di lato 5, e così via.
   • Disposti a spirale, questi quadrati formano un rettangolo che cresce secondo la sequenza.
   • Tracciando archi di quarto di cerchio dentro ciascun quadrato, si ottiene una curva continua: la spirale di Fibonacci.

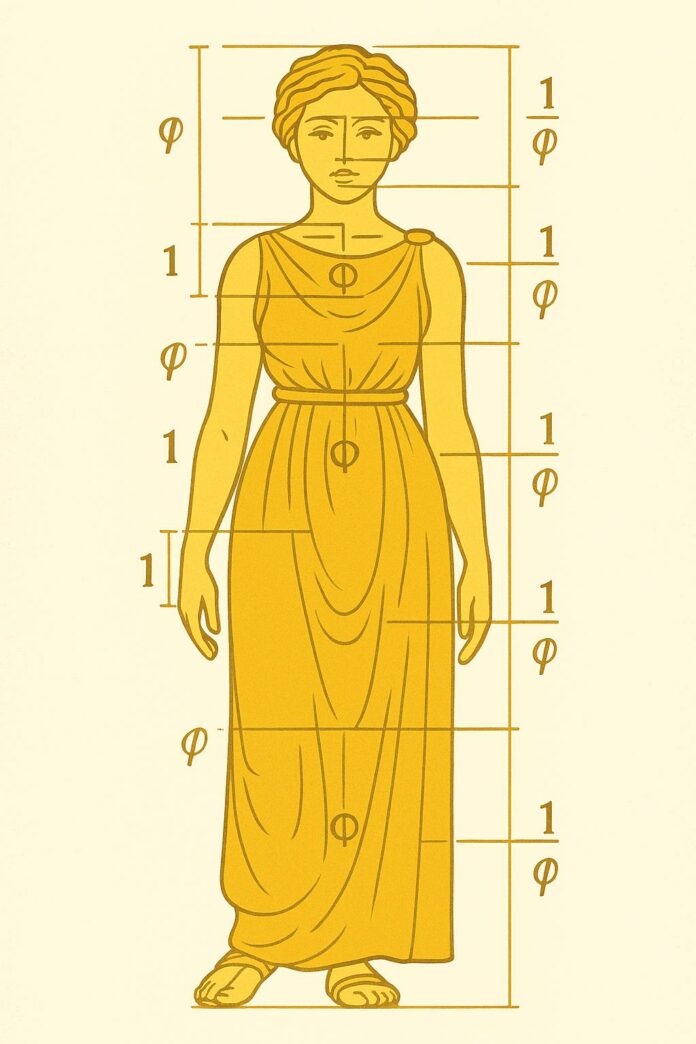
La spirale di Fibonacci approssima la “spirale aurea” e man mano che i quadrati crescono, la curva si avvicina sempre di più alla spirale aurea perfetta che troviamo in Natura: nelle spirali delle conchiglie, nelle corna degli animali, nella forma delle galassie, nella disposizione dei semi nel girasole, delle pigne, delle foglie e anche in arte dove è usata per creare composizioni armoniose, dalla pittura rinascimentale al design moderno.

La spirale di Fibonacci è la traduzione visiva della sequenza: dai numeri nasce una forma che incarna crescita, armonia e proporzione. È un ponte tra matematica e natura, tra calcolo e bellezza.

per leggere la seconda parte

Riccardo Agresti